AC.MQ <- DR X MQ
ku : në regjistrin MQ vendoset shumëzuesi, në DR vendoset i shumëzueshmi, ndërsa në AC.MQ rezultati.
Le te marrim një shembull
Të realizohet shumezimi i dy numrave te paraqitur në formë binare : Y = 1010; X = 1101
Algoritmi i mesipërm nuk ështe shumë i përshtatshëm, pasi duhet qe produktet xj2iY te memorizohen deri në mbledhjen përfundimtare të tyre. Prandaj, në një kompjuter, për realizimin e operacionit të shumëzimit, çdo term i ri xj2iY i shtohet shumës së produkteve të mëparëshme, te cilët quhen produkte të pjesëshme. Në këtë rast mjafton të memorizohet vetëm kjo shumë. Sipas kësaj ideje, algorimi i mësipërm do të merrte formen
pra do të kemi që : Pi+1 = Pi + xj 2iY
Termi 2iY është equivalent me zhvendosjen me i pozicione majtas të numërit Y. Pra, si konkluzion, mund të themi se operacioni shumëzimit reduktohet në zhvendosje majtas të shumëzueshmit Y dhe mbledhje te produkteve të pjesëshëm.Në praktikë kjo ide realizohet pak më ndryshe :
Produktet e pjesëshme Pi , që memorizohen në regjistrin AC.MQ, zhvendosen djathtas duke ruajtur të shumëzueshmin Y, që ndodhet në regjistrin DR, të palëvizur. Pra do të kemi:
Pi ← Pi + xj Y ; Pi+1 = 2-jPi
Shënja e rezultatit do të përcaktohet nga relacioni:p0 = x0 Exlusive OR y0
Si realizohet praktikisht kjo metodë në një ALU:
Për këtë shikoni ketu





.jpg)
.jpg)



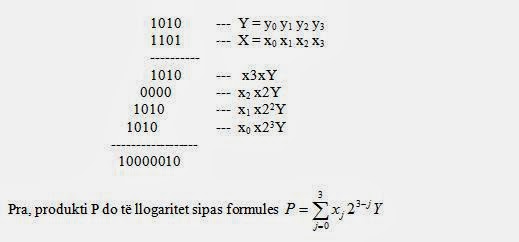











.jpg)
